The Stuff of Genius
Stories about ancient cultures, bakers and Byzantine generals helped Leslie Lamport, MA’63, PhD’72, H’17, explain his visionary ideas and develop the formulas for modern computing.

Peter Strain
Leslie Lamport, MA’63, PhD’72, H’17
by Lawrence Goodman
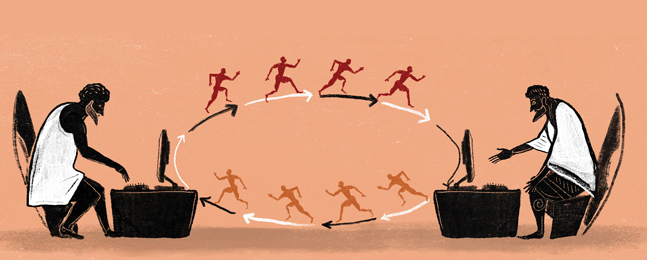
In the late 1980s, computer scientist Leslie Lamport, MA’63, PhD’72, H’17, decided the best way to explain his latest theory was to make up a story about Paxos, a small island in Greece.
During ancient times, Paxos was a busy commercial center with a flourishing democracy, Lamport wrote in an academic paper. Unfortunately, its parliament was hobbled by what Lamport called the “peripatetic propensity of its part-time legislators.” Legislators would abruptly depart whenever they learned of a business opportunity on another island. In addition, poor acoustics in the parliamentary chamber meant lawmakers who were there couldn’t always hear if a vote had been taken.
Luckily, Lamport wrote, Paxos had achieved significant advances in mathematics. And so the tiny island determined the minimum number of legislators needed to establish a quorum. To ensure parliamentarians in the chamber knew about the last vote taken, it calculated routes for messengers to take between them. As a result, legislators might come and go, but there would always be a set number present who knew what was happening.
When Lamport delivered his first lecture on Paxos to colleagues, he dressed up like Indiana Jones, complete with fedora and hip flask, pretending to be an archaeologist who’d dug up remnants of this lost civilization. Not surprisingly, his colleagues thought it was all a joke. Lamport submitted his Paxos paper to a computer science journal, which rejected it as insignificant.
Nearly a decade passed before the journal reconsidered its decision and published the paper. Computer scientists now grasped the story’s significance. Parliament represented a computer network. The legislators were individual computers. The messages were the communications between the computers. Paxos’ mathematical formulas were a method for keeping a network running even as computers joined or went offline.
Today, critical computer systems at Microsoft, Google and Amazon all depend on the Paxos algorithm, a series of mathematical instructions derived by Lamport, who currently works at Microsoft Research in Silicon Valley and received an honorary degree from Brandeis in May.
The Paxos algorithm has made it possible for millions of computers to connect and communicate with one another. Lamport, says Brandeis computer-science professor Liuba Shrira, “originated some of the fundamental concepts behind today’s internet.”
In 2014, he received the A.M. Turing Award, viewed as the Nobel Prize for computer science. In a tribute to Lamport when he got the Turing, internet pioneer Robert Taylor put it bluntly: “You like using the internet, you owe Leslie.”
Problems waiting to be solved
At 76, Lamport is slightly bowed and walks with a small shuffle. Soft-spoken and mild-mannered, he chooses his words carefully and precisely, saying exactly what he must to make his point, then stopping. He’s comfortable with short pauses in conversation.
And then there’s his hair, a bushy white mane that makes him instantly identifiable. He’s worn it in the same style for decades, though it used to be thicker, darker and a little more kempt.
The work for which Lamport is best known focuses on a single question: How do you get computers to talk to one another efficiently and reliably? The question is harder than it sounds. Tens of thousands of computers exchanging millions of messages and executing tens of millions of interrelated functions is a recipe for chaos. Some kind of order must be imposed. The computers must operate in logical sequence.
A simple network consists of several computers calling in to a central server. But you wouldn’t want the computers of tens of thousands of World of Warcraft addicts calling in to the same server at once. One server wouldn’t be able to keep up with all the requests.
To do that, you need a distributed network, the kind of network Lamport researches. A distributed network isn’t arrayed around a single server. Instead, multiple computers talk to one another. Although each computer operates independently, the overall network behavior is coherent. This coherence is achieved through algorithms. When the algorithms are executed across the network, computers coordinate with maximum efficiency and functionality.
Lamport’s tendency to see computer networks as mathematical problems waiting to be solved sets him apart from many computer scientists who focus on mastering specific computer languages, like Java or HTML. Math is more fundamental, Lamport says. It’s the edifice on which the languages stand. College computer-science majors need to learn math, he says, not programming languages that will be obsolete in a few years.
When Lamport started his professional career in the 1970s, computers ran on a few dozen kilobytes of memory. ARPANET, an early progenitor of the internet developed by the U.S. Department of Defense, consisted of roughly 50 terminals writing to reel-to-reel magnetic tape mounted on several mainframe computers.
Lamport’s algorithms anticipated the time when millions of computers would be interconnected. In retrospect, it’s amazing how forward-looking his research was. Martín Abadi, a principal scientist at Google who collaborated with Lamport during the 1980s and ’90s, says that’s because he excels at understanding the large abstract principles at work in computer science, then finding a way to make the abstractions concrete enough to manipulate and apply.
Peter Strain
page 2 of 3
“Leslie is extremely good at taking what might seem an intractable or ill-defined problem and turning it into something tractable,” Abadi says.
“I never had any grand idea of the future,” says Lamport. “I’m not sure anything that’s happened in my life was a conscious decision.” He says he simply goes where his intellectual curiosity takes him, choosing projects that strike him as fun.
To him, solving a problem is akin to completing a seemingly impossible jigsaw puzzle, though he prefers a different metaphor. “The feeling of figuring it out is very much like being in bed after you’ve had an orgasm,” he says. “There’s a wonderful feeling that you’ve done it, and you’re sort of basking in it.”
Bulking up on math
Lamport grew up lower-middle-class in the Bronx. Although his father planned to become a doctor, when the Depression came he took a job at a dry-cleaning company; his co-workers called him Doc. Lamport’s mother was a milliner-turned-housewife.
Their son attended the Bronx High School of Science, one of the city’s best public schools, open to those who pass a rigorous entrance exam. As a junior, Lamport published his first scholarly paper, an article on braid theory, in the school’s Math Journal. With a friend, he attempted to build a 4-bit computer out of discarded vacuum tubes scrounged from an IBM showroom in mid-Manhattan.
Lamport’s real introduction to computers took place during his summers working at the electric company Con Edison. Officially, his job was changing the magnetic tapes used to store data in hulking mainframe computers. But when everyone else went to lunch, he grabbed a computer and taught himself to program.
As an undergrad at MIT, he roomed with George Lakoff, who went on to become a pre-eminent linguist and is now an emeritus professor of cognitive science and linguistics at the University of California, Berkeley. Lakoff remembers Lamport arrived at MIT “very, very skinny and wimpy” yet determined to bulk up. He started sailing, learned karate and cross-country skied in Vermont on weekends. Lamport “would take up something, and could really do it, and do it, and do it,” Lakoff says.
A math major, Lamport regularly pulled all-nighters in a basement computer lab. Lakoff says no matter how arcane or technical the problem, Lamport always wanted to know “what does this mean to human life? He was trying to make sense of mathematics.”
Entering grad school at Brandeis in 1960, Lamport took classes with Richard Palais, a renowned geometry expert, now professor emeritus at Brandeis and adjunct professor of math at the University of California, Irvine. Lamport admired Palais’ rigor, and the elegance and simplicity of the theorems he developed. “I don’t know whether he thought like I thought or he taught me to think like him,” Lamport says, but Palais “had a mind that was very simpatico to my own.” The two remain friends.
Yet Lamport often felt adrift. “I wasn’t studying,” he says. After getting his master’s, he left Brandeis to teach at Marlboro College, in Vermont. What was his experience like there? “Recall that it was the ’60s,” he says. “Enough said.” Eventually, his passion for learning returned, and he came back to Brandeis to get his doctorate.
In 1970, while still working on his PhD, Lamport joined Massachusetts Computer Associates, a now-defunct software company outside Boston. His supervisors gave him free rein to do what he wanted. “The people I was working for saw I was pretty smart and I could do things if they left me alone,” he says.
The bakery algorithm’s sweet spot
Only a few years earlier, the Dutch computer scientist Edsger Dijkstra had posed what became known as the mutual exclusion problem. Take two networked computers, press “print” on both of them, and you’re liable to have a logjam, because the printer can handle only one file at a time. Dijkstra realized a system was needed to ensure computers took turns, a system that ensured mutual exclusivity. When a computer was using a shared resource like a printer or a hard drive, no other computer would be able to gain access.
In a 1974 paper, Lamport announced his solution to the mutual exclusion problem. It had dawned on him that computers trying to access a printer simultaneously were a lot like bakery customers demanding to be served. As a kid, he’d lived near a bakery. People came in, took a numbered ticket and waited until their number was called. The earlier you arrived, the lower the number on your ticket.
Like customers, computers needed to be assigned a number and then called when their number came up. The tricky part is that distributed networks don’t have a central server — that is, a single ticket counter — the computers can check. So Lamport devised an algorithm that gets a computer to ask the other computers in the network for their numbers. It then assigns itself a higher number than all the rest. The “bakery algorithm” achieved fairness: Computers are waited upon on a first-come, first-served basis.
Lamport spent the next several years exploring the bakery algorithm further before achieving the breakthrough that vaulted him to fame in his field. He started thinking about time. Clocks on a computer are often inaccurate, perhaps because the time was set wrong or because of “clock drift,” where even the most precise timing device eventually becomes inaccurate.
There was another problem: Computers may have weak processors or slow internet connections. Suppose two computers try to print. One sends its request first, but if the other computer has a better chip or a better router, its request could reach the printer faster.
So Lamport decided to throw real-world clocks out the window. Instead, a computer network would keep its own “time,” based on mathematical logic. If computer B receives a message from computer A, computer B determines computer A comes before it. If computer C receives a message from computer B, it determines computer B comes before it. Computer C can go a step further on the basis of the law of syllogism — if A comes before B and B comes before C, you can logically assume that A comes before C, too.

Peter Strain
page 3 of 3
As messages are exchanged across the network, these if-then statements give rise to an overall order. This system became known as a “logical clock,” and “Lamport timestamps” assigned each computer a number in line.
The paper Lamport eventually published about this, “Time, Clocks and the Ordering of Events in a Distributed System,” remains one of the most cited in the computer science field.
Battle ready
During the 1980s, Lamport achieved more stunning breakthroughs. He developed LaTeX (an abbreviation of Lamport TeX), a plain-text editor ideal for typesetting mathematical equations. “It’s quite incredible how widely used LaTeX still is,” says Justin Boyan, a computer scientist and former product manager at Google. “Literally multiple generations of software have come and gone while LaTeX keeps chugging along.”
And in 1982, Lamport and colleagues Marshall Pease and Robert Shostak devised a solution to the “Byzantine generals problem.” Imagine a group of generals who’ve camped at different locations around an enemy city. Their opponent is fierce and can be defeated only if the generals attack together. The generals dispatch messengers to find out the exact time the assault will happen. But there are traitors in their midst: Some messages may report a wrong time of attack, ensuring defeat. The good news is that each general receives some true messages from loyal generals. The challenge is to weed out a false message after receiving as few messages as possible.
In this problem, the “traitors” are computers that go on the fritz, perhaps because of a software bug or malfunctioning hardware. A faulty message sent by a computer can crash a network. Like the generals, the computers in the network must discern the bogus communications and continue operating on the basis of the legitimate ones. They do this by comparing the messages they’ve received and using a set of conditions and criteria to determine which are the most shared among them. The outliers are then judged as faulty or deceptive, and ignored.
The risk of traitors operating in a computer network is constant, and their presence can prove lethal — literally. If a hospital computer malfunctions, patients may die. If a computer in an air-traffic control system goes haywire, airplanes may crash. These systems and many others rely on Lamport’s solution to remain operative in the wake of breakdowns.
Think before you code
In 2005, just weeks before Microsoft unveiled the Xbox 360, a Microsoft intern was asked to check the game console’s programming for bugs. He ran the software code through a rigorous analytical process called the temporal logic of actions (TLA+), developed by Lamport when he joined Microsoft Research several years earlier.
Sure enough, the TLA+ check uncovered a serious bug. If it hadn’t been caught, every single Xbox would have crashed after only four hours of use.
Lamport developed TLA+ as part of a larger crusade to get his colleagues to think better. Programmers, he says, sometimes write code without asking themselves big questions. What do they want their program to do? How should it do those things?
TLA+ brings to programming the rigor and precision that mathematical proofs demand. Before you start writing software code, you create an outline, expressed in mathematical theorems, that explains what your program will do and how it will do it. You lay out the big concepts at work in the software, then demonstrate that they will function together successfully.
Given the competitive and financial pressures many software engineers work under, they often feel they don’t have time to step back and examine the big picture. But Lamport says the failure to answer big questions first results in software written ad hoc. Programmers scramble to figure out their objectives. Inevitably, bugs creep in. The code becomes sloppy and bloated.
“Architects draw detailed plans before a brick is laid or a nail is hammered. Programmers and software engineers don’t,” Lamport wrote in a 2013 article in Wired magazine. “Can this be why houses seldom collapse and programs often crash?”
You can’t possibly test software for every possible contingency before it’s released. Once users start putting it through its paces, all sorts of bugs will emerge. But if its underlying logic is sound, there’s a much better chance it can handle whatever users throw at it. TLA+ helps prove the underlying logic is sound.
Lamport’s address to Brandeis computer-science graduates at this year’s Commencement was characteristically modest and witty. He cited what he calls Lamport’s Law — “the abilities required to obtain a position are unrelated to the abilities required to do a good job in that position” — then added, “I don’t think there’s any need for me to explain how this law applies to American politics today.”
He offered graduates one piece of advice: learn to write. He makes the same suggestion in talks to colleagues, often citing the cartoonist Dick Guindon: “Writing is nature’s way of letting you know how sloppy your thinking is.” Through the crucible of writing, thoughts obtain clarity and precision.
At the beginning of his Brandeis address, Lamport promised to limit his speaking time to eight minutes. He was unsure, he said, “if I can even keep you awake for the next six minutes and 40 seconds.”
When eight minutes had passed, his watch alarm sounded. “I’m afraid that’s all the inspiration I have to offer,” he said.
Most likely, it will last generations.
