Optimization of a Granular Structure
Undergraduates Edwin Faican, Remi Boros and Pranav Gupta (IISc, Bangalore) presented posters at Brandeis SciFest 2014. (Faican/Boros/Chakraborty).
As seen on trips to the beach, adding enough water to dry sand allows the creator to form towering sandcastles, while adding too much or too little can lead to premature castle collapses. By taking the experimental data from Daniel Bonn's "How to Perfect a Sandcastle," we found relationships between the heights of sand pillars in relation to their relative water per percentage volume ratios. Using PVC tubing with a 2cm radius, we found the optimum percent volume of water in sand to be 12%.
A sandcastle built underwater. It contains capillary bridges made of air to maintain stability which is possible with hydrophobic sands.
The height of a sand pillar depends on sand density, gravity, pillar radius and the Elastic Modulus. Of these relationships, in this experiment, the density, gravity and pillar radius was held constant.
The Young's Modulus of a material defines the property of a stress per strain relationship. It is a dimensionless quantity that defines the ability of an object to be deformed. In these experiments, Young's Modulus was affected by the material's water concentration. The Elastic Modulus G is a quantity dependant on a material's Young's Modulus E, average radius of particles a, and surface tension y. It defines the ability of an object to deform at a bend from the stability axis.1
- Stronger attractive bonds between particles of granular material.
- The Young's and Elastic moduli increase, allowing for more stable structures, most notably when compressed.
- Segments of granular material can support additional weight, allowing them to rise without buckling
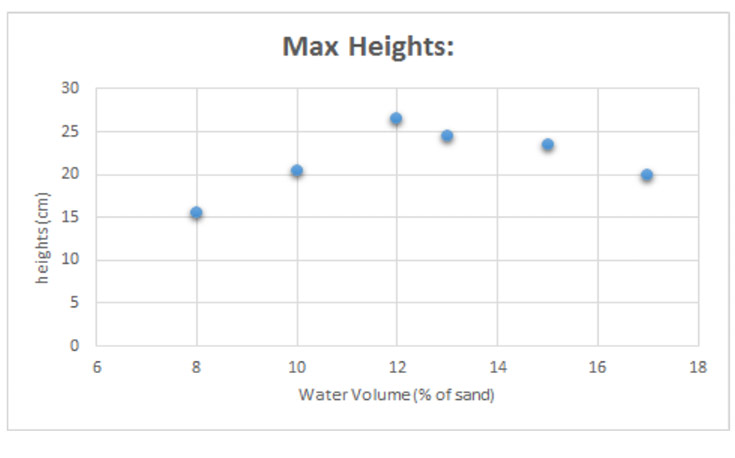
This graph shows the relationship between water volume percentage and maximum height of the granular pillars. There is a distinct peak at around 12% water though the graph is rough due to limited data.
Too much water can easily overwhelm any particle bridging capillary bonds, while too little may not be sufficient in forming stable bonds between every particle. Subsequently, we expected a peak at which the moduli and heights are highest in relation to each specific water volume percentage. A sand pillar's maximum height is theoretically represented by the following formula1: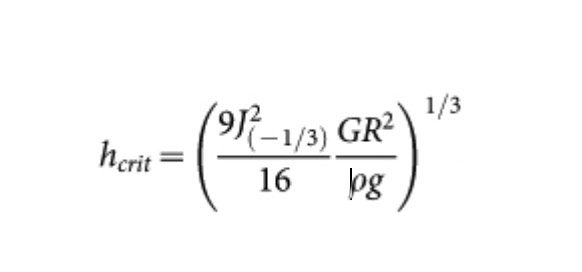
where J, R, ρ, and g are constants. This relates the pillar’s modulus to its height. Using this, we found the sand's elastic modulus for each water concentration after we measured a pillar's critical height.
- Prepare our water and sand mixture at a desired ratio.
- Using a funnel, pour a quantity of this mixture into a 4cm split pipe, leaving a small slot between both pipe halves for ample force dissipation to minimize sand-pipe adhesions.
- By repeatedly dropping a flat, circular metal weight attached to a rod, compress our sand pillar.
- Carefully remove each pipe half, making sure to sever any connections between the pipe and pillar to avoid unnecessary resistive forces.
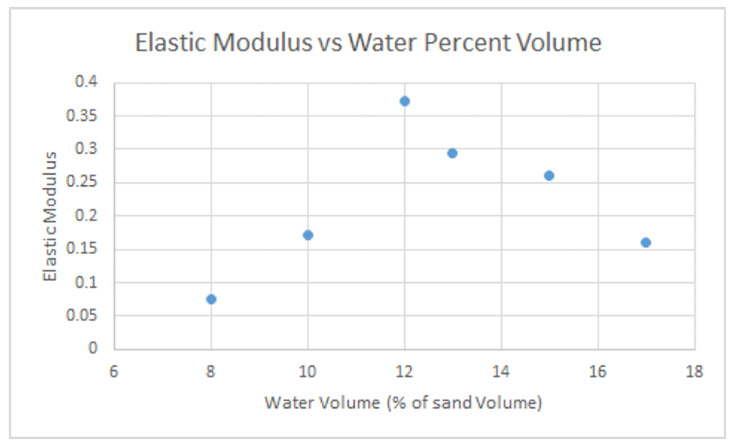
This graph displays the relationship between the elastic modulus and the percent water volume. Similar to Figure 2, this graph also has a peak at 12% suggesting the relationship between height and the modulus.
While the water concentration of our peak height differed greatly from Bonn's (1%), it is undoubtable that we found a prominent maximum at about 12%. This large difference in peak optimum water concentration was most likely affected by the difference between our sand's density (1.6 g/cm3) and Bonn's (2.6 g/cm3). Furthermore, the results displayed on our Elastic Modulus graph allowed for the confirmation of this ideal water volume percentage. The existence of this peak is especially prominent as it not only indicates the physical limitations of granular materials, but furthers our cause in creating the perfect sandcastle.