Dynamical Formation of Empty Viral Capsids
The basic components of a virus are genetic material and a protein shell, called a capsid, that surrounds and protects the fragile nucleic acids.
During the life cycle of a virus, the genetic material is released inside a cell and cellular machinery is hijacked to replicate the viral genome and manufacture new viral proteins. Capsid proteins then assemble with nucleic acid molecules to form new viruses. This process is remarkable because a large number (60 – thousands) of capsid proteins avoid kinetic and thermodynamic traps to assemble rapidly and reliably in many different organisms and environments. Even more remarkably, in vitro studies show that capsid proteins alone can spontaneously assemble into perfectly formed capsids. Assembly therefore can be directed entirely by interactions between individual proteins. How do these local interactions conspire to form robust large length scale assemblies?
Despite the apparent simplicity of a symmetric virus, modeling the kinetics of capsid assembly poses a great challenge. Assembly times and capsid structures are orders of magnitude larger than the length and time scales that characterize individual subunits. Simulations with atomistic resolution are impractical to study assembly dynamics for one or many capsids. Therefore, we designed coarse-grained models with which to study specific questions about the assembly process.
We began with the following question: viral capsid proteins have complex shapes and interact through forces arising from sequences and structures that have evolved over millions of years. What features of these interactions are critical to ensure that system dynamics lead to a free energy minimum (properly formed capsids) rather than metastable disordered states (malformed or incomplete capsids)?
To identify the minimal interactions required for successful assembly, we designed a minimal model for capsid proteins. The model consists of rigid subunits, or "capsomers," with spherically symmetric space filling volumes and directional attractive interactions that represent interactions between complementary interfaces on capsid proteins (see Figure 1).
The lowest energy states in the model correspond to "capsids" comprised of multiples of 60 subunits in a shell with icosahedral symmetry. Dynamics are simulated with non-inertial Brownian dynamics, in which particle motions are calculated from Newton's laws with forces arising from subunit-subunit interactions, hydrodynamic drag, and a random buffeting force.
An important feature of these simulations is that dynamics are time-reversible and satisfy detailed balance. It is precisely these features of real dynamics that would seem to make assembly into well-defined ordered structures unlikely.
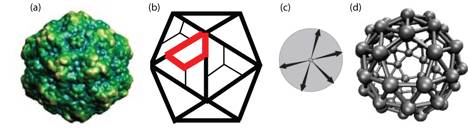
Figure 1: Description of model subunits. (a) An x-ray crystallography image of a canine parvovirus (CPV) capsid (reproduced from Ref. [1]). (b) A schematic drawing that illustrates how capsid proteins, depicted as trapezoids, are arranged in CPV capsids with icosahedral symmetry. A single schematic protein is outlined in red. (c) Illustration of model subunits used in Ref. [2]. Arrows represent directional attractions that mimic complementary interfaces on capsid proteins. (d) The lowest free energy configuration for the model proteins shown in (c). The size of model subunits have been reduced to aid visibility. For a more detailed discussion, see the section entitled "Relation of model capsids to actual viral capsids" in Ref. [2].
The geometry of directional attractions is chosen such that a particular capsid structure is the free energy minimum. Assembly pathways are not pre-assumed in this model, and once the subunit structure is specified there are few remaining adjustable parameters: subunit concentration, binding energy and the angle tolerance for directional attractions. Dynamical simulations were carried out over a wide range of these parameters; some results of these simulations are shown in Figure 2.
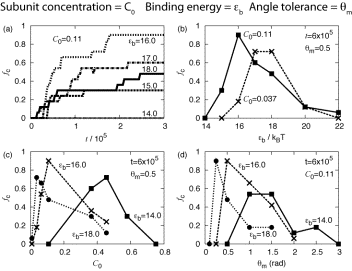
Figure 2: Fraction of subunits in complete capsids, fC, as a function of system parameters. Subunit concentration and time are in reduced units and bond energy is in units of the thermal energy, kBT. At low concentrations and bond energies, capsids do not form within the time simulated. When concentrations or bond energies become too large, however, ordered capsids do not form.
At low subunit concentrations or binding energies, the driving forces for assembly are weak; increasing concentration or binding energy leads to faster and more successful assembly. This trend is nonmonotonic, however; above some optimal parameter values a stronger driving force for assembly leads to less efficient capsid formation. Although capsids are more thermodynamically favored with increasing parameter values, structures with strained bonds or defects also become more stable. As defects become trapped in a growing capsid by further addition of subunits, the thermodynamically stable state becomes kinetically inaccessible.
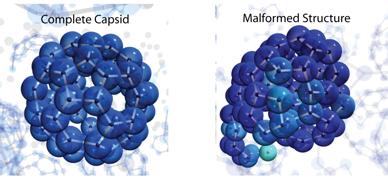
Figure 3: Snapshots from dynamical trajectories. For the case shown on the left, system parameters were such that the dynamics produced a high yield of correctly assembled capsids. For the case on the right, strained bonds were stable enough that they did not anneal before additional subunits bound. Note that a properly assembled capsid is the thermodynamically favorable state in both cases. In fact, the ordered capsid is actually more thermodynamically favored in the case on the right.
References
- Reddy, V.S., et al., Virus Particle Explorer (VIPER), a Website for virus capsid structures and their computational analyses. Journal of Virology, 2001. 75(24): p. 11943-11947.
- Hagan, M.F. and D. Chandler, Dynamic pathways for viral capsid assembly. Biophysical Journal, 2006. 91(1): p. 42-54.
- Jack, R.L., M.F. Hagan, and D. Chandler, Fluctuation-dissipation ratios in the dynamics of self-assembly. Physical Review E, 2007. 76: p. in press.