2013 Research Highlights
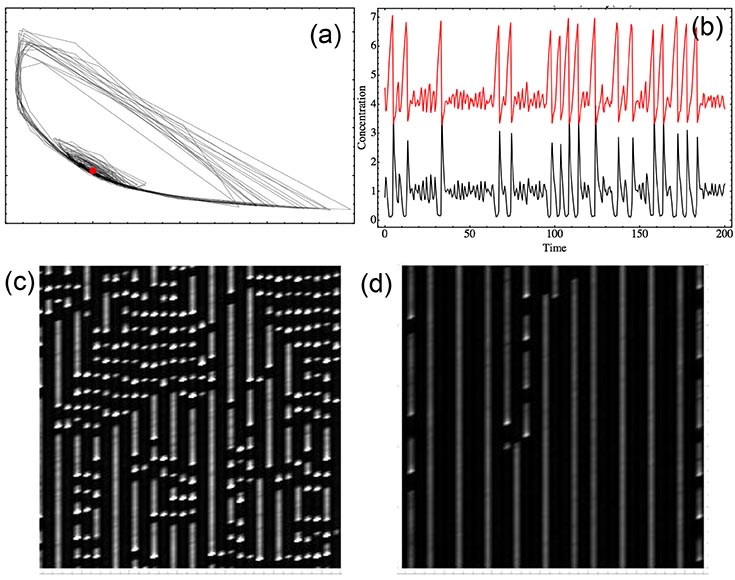
(a) Phase portrait of a single, noisy oscillator, showing a large amplitude relaxation oscillator mixed with a noisy limit cycle surrounding the meanfield fixed point (red dot) (b) A typical time trace showing the mixed mode oscillations (c) Spatio -temporal pattern showing patches of oscillating and stationary regions in a one dimensional array of diffusively coupled oscillators . Horizontal axis denotes space and vertical axis denotes time . (d) As the ration of inhibitor to activator diffusion constant is increased, the patchy, oscillating phase changes to a stationary Turing pattern
Intrinsic noise has been shown to play an important role in the dynamics of a variety of systems including predator-prey populations, intracellular biochemical reactions, and oscillatory chemical reaction systems. Computer Simulations of the Brusselator, a prototypical chemical oscillator, predicts the existence of mixed mode oscillations, even for a large number of molecules, when there is a large separation of time scales between the dynamics of the inhibitor and activator species. (a) Phase portrait of a single, noisy oscillator, showing a large amplitude relaxation oscillator mixed with a noisy limit cycle surrounding the meanfield fixed point (red dot) (b) A typical time trace showing the mixed mode oscillations (c) Spatio-temporal pattern showing patches of oscillating and stationary regions in a one dimensional array of diffusively coupled oscillators. Horizontal axis denotes space and vertical axis denotes time. (d) As the ration of inhibitor to activator diffusion constant is increased, the patchy, oscillating phase changes to a stationary Turing pattern.
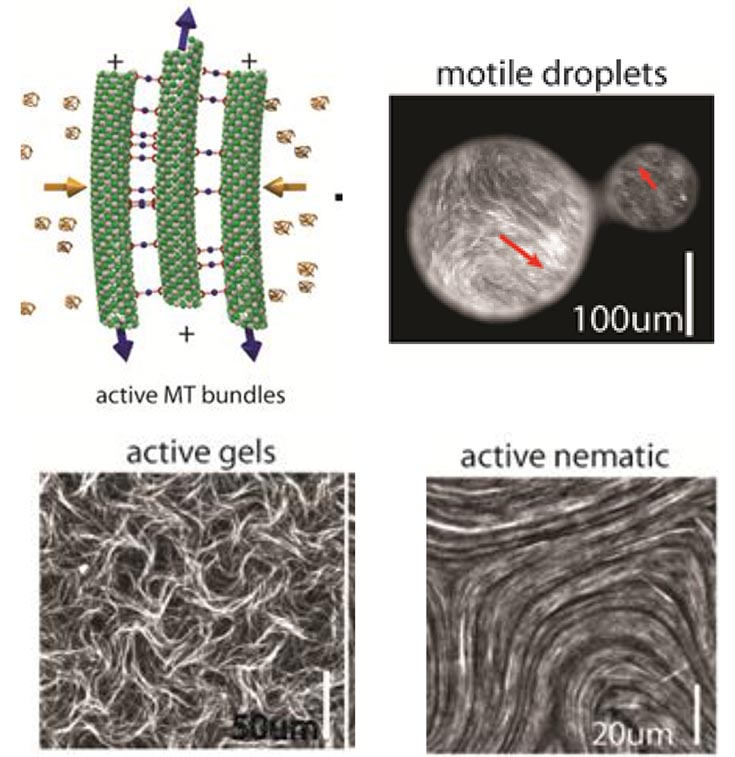
Most conventional materials are assembled from inanimate building blocks. We have explored the behavior of soft materials in which constituent energy consuming units are assembled from animate energy consuming components. Thousands of these components spontaneously coordinate their microscopic activity to yield novel gels, liquid crystals and emulsions that crawl, flow, stream, spontaneously fracture and selfheal, thus mimicking some of the characteristics of living biological organisms.
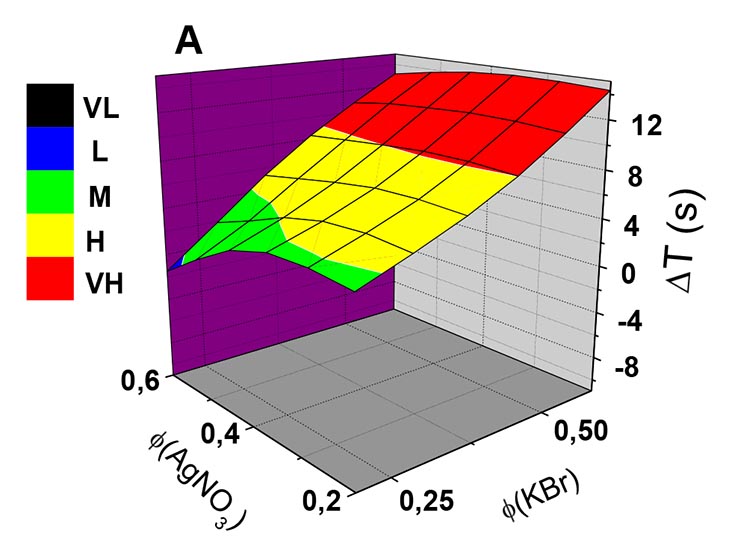
Fig: Three-dimensional representation of a fuzzy logic system based on V(KBr) and V(AgNO3 ) as inputs and ΔT as output at three different phases of chemical injection: φ = 0.2 (A), 0.4 (B), 0.6 (C). The output fuzzy sets are represented by colors as indicated in the sidebar at the left.
The oscillatory Belousov-Zhabotinsky (BZ) reaction can be exploited to process both Boolean and fuzzy logic if the input variables are either the volumes or the phase of addition of pulse-injected solutions of inhibitor (bromide) and activator (silver ion) and the output variable is the oscillation period. Our experiments demonstrate that this system can process infinite-valued fuzzy logic, and that all fundamental fuzzy logic operators (AND, OR, NOT) can be implemented with it. This work suggests the possibility that biological oscillators such as neurons or pacemaker cells may process information using principles of fuzzy logic.
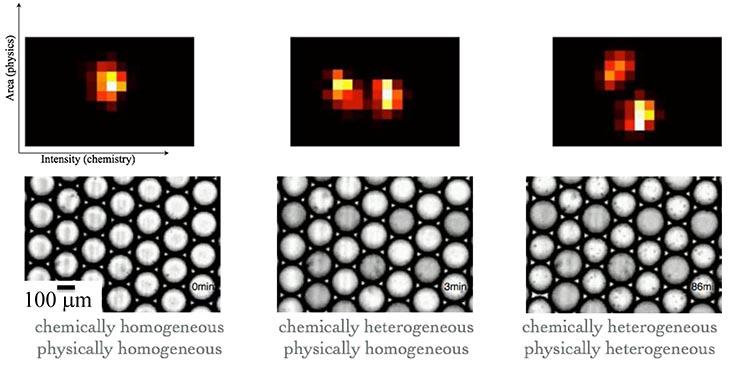
In this work we study the emergence of chemical and physical heterogeneity from an initially homogenous system. We use an emulsion containing the Belousov-Zhabotinsky (BZ) reaction which undergoes pattern formation and eventually morphogenesis. Using the Turing mechanism we are able to characterize the patterns formed at an analytical level.
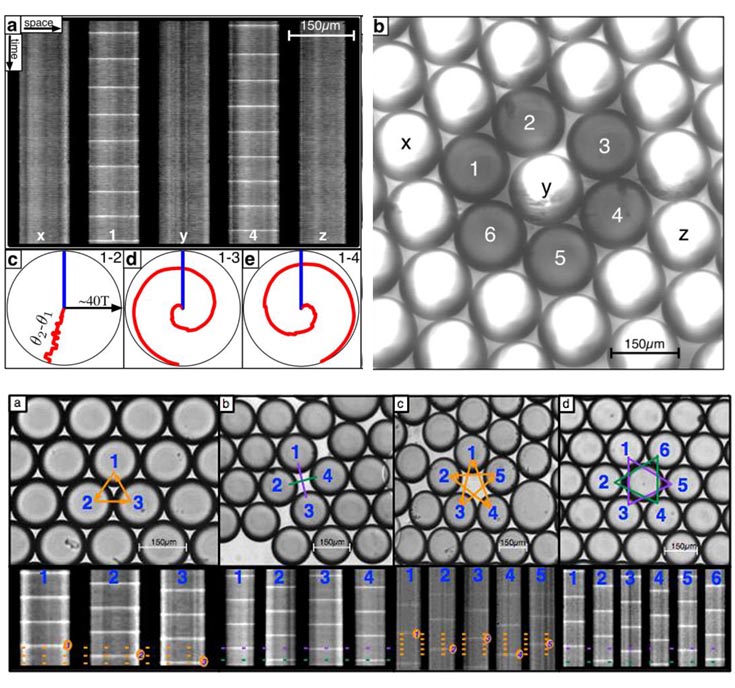
In this work we use a photosensitive form of the Belousov-Zhabotinsky (BZ) reaction and a Programmable Illumination Microscope (PIM) to create optical boundaries conditions within an emulsion. This allows us to create geometries of cellular oscillators with only nearest neighbor coupling. By creating 1D rings we can test the effects of having an even or odd number of drops. The different behavior from identical conditions can be used to help in the creation of customized materials.
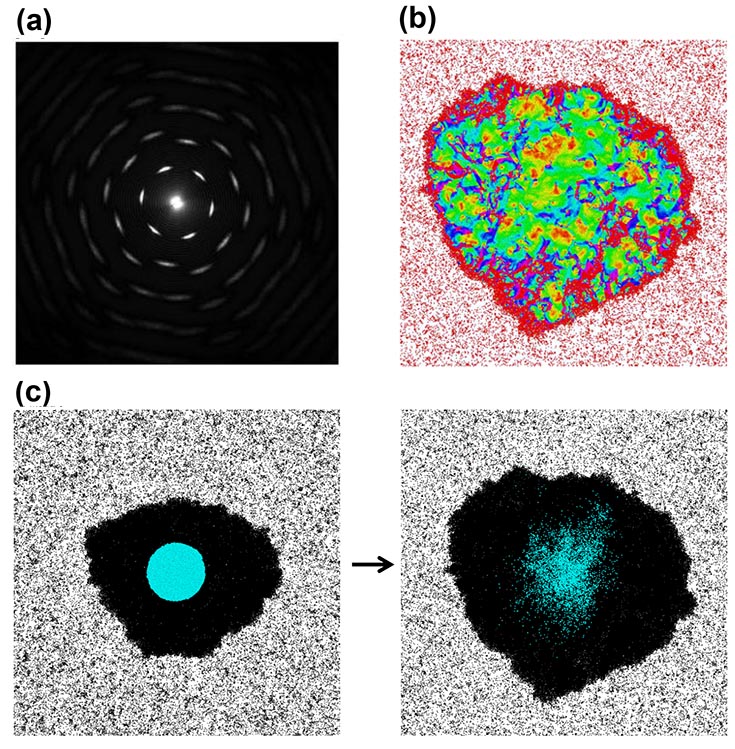
Computer simulations of self propelled spheres in 2d predict a new form of matter: an active liquid crystal. (a) The structure factor for an example active crystal showing crystallinity. (b) Instantaneous speed of particles within the system, illustrating the inhomogeneous motion within the crystal. (c) Particles in the active crystal undergo diffusion. The image shows the analog of a FRAP experiment. The particles which start in the center are labeled blue; the image to the right shows a snapshot after evolution of the dynamics.
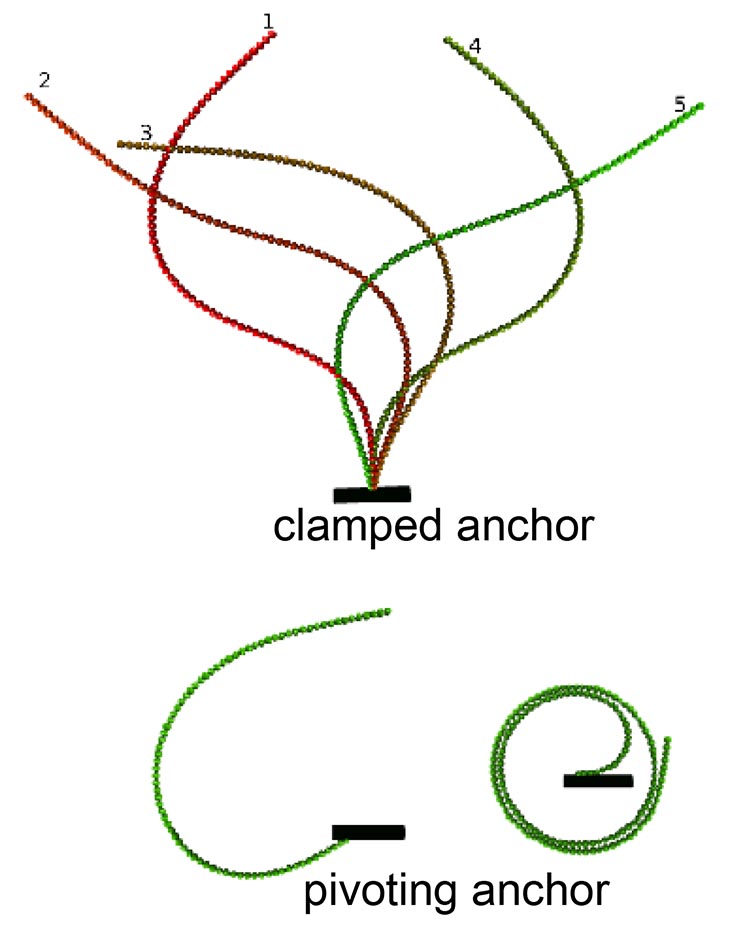
Filament configurations at different times are shown in different colors. Upper diagram: Clamped anchor. Lower diagram: pivoting anchor. Filament configurations at different times are shown in different colors. Upper diagram: Clamped anchor. Lower diagram: pivoting anchor.
The planar dynamics of a semi-flexible filament anchored at one end and comprised of connected, self-propelled, spheres were predicted using Brownian dynamics simulations and continuum elastic theory theory. For certain parameter ranges the filament undergoes periodic motion. With a clamped anchor, the filament undergoes flagella-like beating (top right), while a pivoting end leads to a steadily rotating coiled conformation (bottom right).
Designing simple, experimentally feasible systems that mimic the periodic beating of eukaryotic cilia and flagella has important implications for controlling fluid flow at the microscale, as well as for understanding biological cilia and flagella.
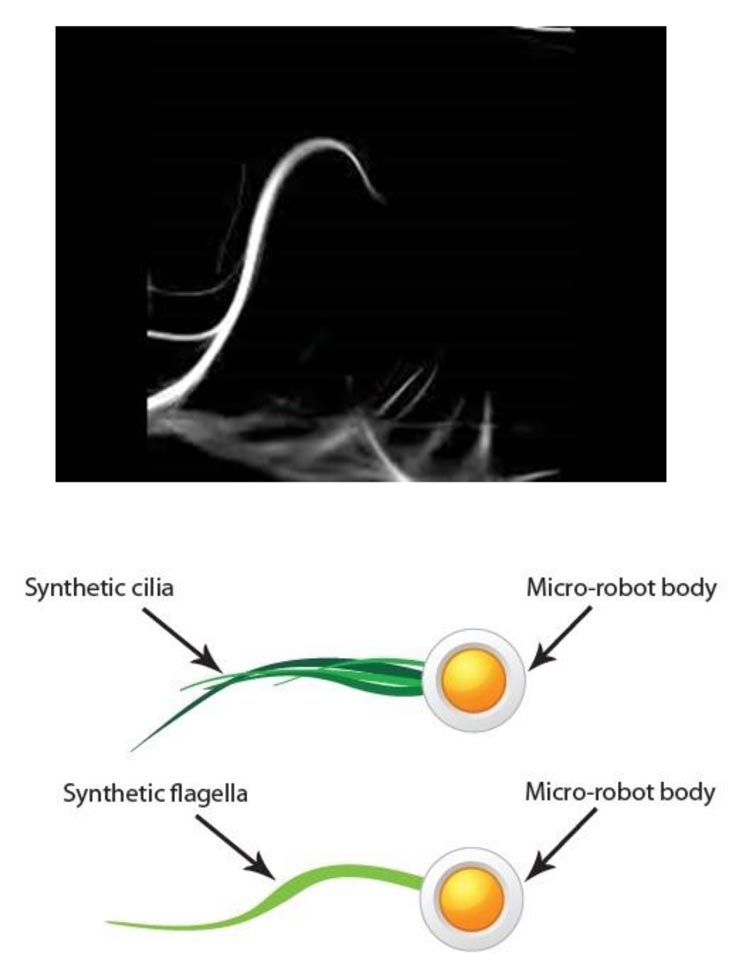
Top: Synthetic cilia composed of microtubule bundles. Bottom: Conceptual diagram of micro-robots propelled by synthetic cilia and flagella.
The goal of this project is to build swimming micro-robots composed of a microrobot body and synthetic filamentous bundles powered by molecular motors that exhibit periodic beating patterns similar to those of biological cilia. We are exploring methods to attach the synthetic cilia to a micron sized robot body which will behave as a molecular swimmer that mimics the behavior of biological spermatozoa. An autonomously powered micro-robot with tunable and controllable beating patterns would provide an ideal system to deliver a therapeutic drug to a cancerous tissue.
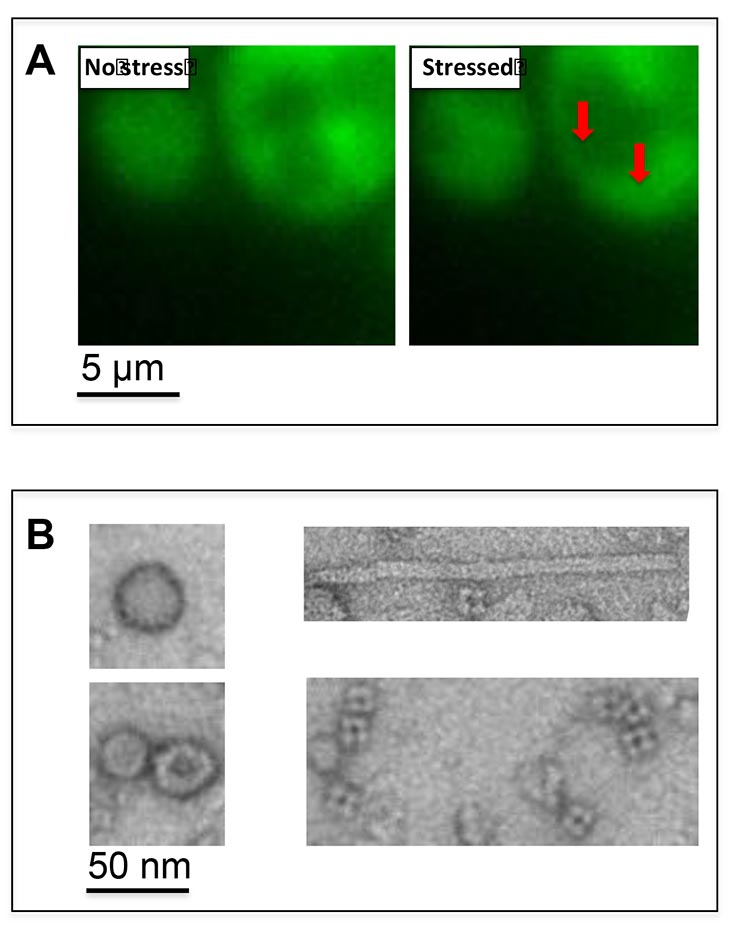
Figure A: 5um. Left: No stress. Right: Stressed. Figure B: 50 nm
Eukaryotic cells possess poorly understood nonmembrane enclosed subcellular organelles that are sites of activity critical to post-transcriptional gene regulation. We are studying a subcellular organelle called a stress granule, which are large (~150 nm diameter) and dynamic stress induced cytoplasmic aggregates.
Our studies include both the characterization of stress granule dynamics in cells using live cell imaging techniques (see “A”, top right) as well as studies in vitro of the protein components that are integral to the assembly of stress granules (see “B”, electron microscopy micrographs bottom right).
We are quantifying the dynamics of stress granules and elucidating the principles and components underlying their assembly to form stress granules.

